[JAVA] 플로이드-워셜 알고리즘

 플로이드-워셜 알고리즘

 

그래프에서, 한 정점에서 다른 정점으로 가는 최단거리가 있다.

플로이드-워셜 알고리즘을 사용한다면 각각의 모든 정점에서 모든 정점으로 가는 최단거리를 전부 구할 수 있다.

 

 

 

즉, 1 ~ 2, 1 ~ 3, 1 ~ N

2 ~ N

3 ~ N

4 ~ N

5 ~ N

모든 경로에서 전부 최단 거리를 구할 수 있다.

 

2 -> 1로 가는 최단 경로를 볼 때,

2 -> 1은 9

2 -> 3 -> 1은 7로 노드 3을 거쳐가는 것이 더 빠름

 

이렇게 노드를 거쳐서 가는게 더 빠른 경로까지도 플루이드-워셜 알고리즘을 통해 구할 수 있다는 것이다.

 

 

 

 

플로이드-워셜 알고리즘은 DP(Dynamic Programming) 기법을 사용한 알고리즘이다.

즉, 노드 0개를 거쳐가는 최단거리를 구하고, 노드 1개, 노드 2개...노드 N개를 거쳐가는 최단거리를 '단계적'으로 수행하며 기존 값보다 더 최단거리가 나오면 값을 갱신하는 방식이다.

 

 플로이드-워셜 알고리즘 : 그림을 통한 접근

 

그렇다면 간단하게 그림을 통해 플로이드-워셜 알고리즘을 살펴보자.

원래라면 노드 0~4개까지 거쳐가는 최단거리를 다 구해봐야 하지만, 간단하게 노드 0~1개까지 거쳐가는 경로까지만 알아보도록 하자. (이 경우까지만 봐도 그 이후까지 감을 잡을 수 있을 것이다.)

 

위의 그래프를 보며 인접행렬을 만들어보자. 이 알고리즘은 인접행렬이 필요한 문제다.

(인접행렬을 모르는 경우 이곳을 클릭해서 먼저 보고오자.) 

 

 

 

 

 

 

먼저 노드, 0개를 거쳐가는 경우다.

이 때는 자기 자신을 가는 경우 뿐이니 자기 자신에 가중치 0을 대입한다.

 

 

 

 

 

 

 

 

노드 1개를 거쳐가는 경우다.

1->2 한번 거쳐가는 경우 : 9

1->3 한번 거쳐가는 경우 : 2

1->4 한번 거쳐가는 경우 : 4

1->5는 한번에 가는 방법이 없으니 INF그대로 놔둔다.

 

행렬[a][b]값에 가중치를 넣기 전, 기존 값보다 작은 경우에만 값을 바꿔준다. 

결론적으로 최단 거리를 구해야 하기 때문

 

 

 

 

 

 

 

노드 2개를 거쳐가는 경우다.

1->3->2 : 7

기존 1->2로 가는 경로보다 빠르니 대체한다.

 

2->1->3 : 11

기존 2->3 : 5 이므로 값을 갱신하지 않는다.

 

이런 방식으로 모든 노드를 진행하면 왼쪽 행렬과 같이 갱신된다.

 

 

 

이러한 방식으로 노드를 N번 거쳐가는 경우까지 비교하여 갱신하면

모든 노드가 최단거리로 목적지 노드로 가는 경우를 구할 수 있다.

이것이 플로이드-워셜 알고리즘이다.

 

 플로이드-워셜 알고리즘 : 코드 구현

 

그림으로 방식을 이해했으니 이제 코드를 통한 구현을 살펴보자.

 

 

public class Main {

    public static void print(int[][] graph) {
        for (int i = 1; i < graph.length; i++) {
            for (int j = 1; j < graph.length; j++) {
                if (graph[i][j] == 999_999_999)
                    System.out.print("INF ");
                else
                    System.out.print(graph[i][j] + " ");
            }
            System.out.println();
        }
    }

    public static void putEdge(int[][] graph, int x, int y, int edge) {
        graph[x][y] = edge;
        graph[y][x] = edge;
    }

    public static void main(String[] args) {
        int n = 5; //그래프 정점의 개수
        int[][] graph = new int[n+1][n+1]; //index를 1부터 맞추기 위해 n+1

        putEdge(graph, 1, 2, 9);
        putEdge(graph, 1, 3, 2);
        putEdge(graph, 1, 4, 4);
        putEdge(graph, 2, 3, 5);
        putEdge(graph, 2, 5, 7);
        putEdge(graph, 3, 4, 1);
        putEdge(graph, 4, 5, 8);

        System.out.println("주어진 그래프의 모양");
        print(graph); //주어진 그래프다.
        System.out.println();

        int[][] floyd = new int[n+1][n+1];
        for (int i = 1; i < floyd.length; i++) {
            for (int j = 1; j < floyd.length; j++) {
                if (i == j)
                    floyd[i][j] = 0; //노드를 0개 거쳐가는 경우는 자기 자신뿐이다.
                else //불가능한 경우는 매우 큰값을 넣는다. 모든 노드를 거쳐간 값보다도 클 수 있도록
                    floyd[i][j] = 999_999_999;
            }
        }
        // 주어진 가중치 값을 집어넣는다. 즉, 노드를 1개 거쳐가는 경우를 넣는다.
        putEdge(floyd, 1, 2, 9);
        putEdge(floyd, 1, 3, 2);
        putEdge(floyd, 1, 4, 4);
        putEdge(floyd, 2, 3, 5);
        putEdge(floyd, 2, 5, 7);
        putEdge(floyd, 3, 4, 1);
        putEdge(floyd, 4, 5, 8);

        // 플루이드-워셜 알고리즘 실행
        for (int i = 1; i < floyd.length; i++) {
            for (int j = 1; j < floyd.length; j++) {
                for (int k = 1; k < floyd.length; k++) {
                    // 기존 j -> k까지의 거리와, i번째 노드를 거쳐가는 거리를 비교해 최단거리 갱신
                    floyd[j][k] = Math.min(floyd[j][k], floyd[j][i] + floyd[i][k]);
                }
            }
        }

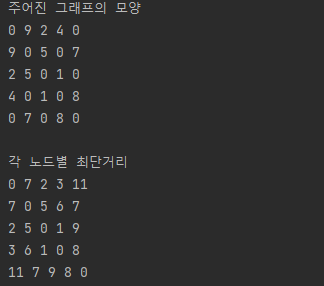
실행결과는 다음과 같다.

 

예시는 위의 그래프로 진행하였으니

실제로 각 노드별 최단거리가 구해졌는지 쉽게 확인 가능하다.

 

(왜 i j k순이 아니라 j i k순일까?)

그 이유는 우리가 비교해야 할 대표 값은 거쳐가는 노드 i다.

거쳐가는 노드 i를 두고 j -> i -> k에서 j와 k 값을 바꾸며 

최단거리를 구해야 하기 때문

 

 

 

코드를 보면 다소 어지러운 삼중포문이 보인다. 즉, 수행속도가 O(N^3)이라는 뜻이다.

따라서 주어진 값들의 크기를 잘 살펴보고, 크기가 수행하기 적절한 경우에만 이 알고리즘을 사용하는게 좋을 것이다.