2022. 3. 19. 01:29ㆍ알고리즘/프로그래머스
문제 링크
https://programmers.co.kr/learn/courses/30/lessons/43238
코딩테스트 연습 - 입국심사
n명이 입국심사를 위해 줄을 서서 기다리고 있습니다. 각 입국심사대에 있는 심사관마다 심사하는데 걸리는 시간은 다릅니다. 처음에 모든 심사대는 비어있습니다. 한 심사대에서는 동시에 한
programmers.co.kr
문제의 제한사항을 보면 1,000,000,000이라는 택도없이 큰 숫자가 등장한다.
보통 제한사항의 숫자가 큰 경우에는 완전탐색등의 방법을 쓰면 경우의 수가 어마무시하게 커지게 될 것이다.
이런 경우에는 효율적인 알고리즘을 채택해야 하는데, 필자는 이 문제에서 '이분 탐색'을 선택했다.
이분 탐색
이분 탐색은 일련의 데이터들 중에서 하나의 값을 찾을 때, 처음부터 세지 않고 '탐색 범위를 반으로 나누어' 찾는 방식이다.
그림을 통해 간단히 확인해보자.
탐색을 계속하는 조건은 left < right이다.
(left : 탐색을 시작하는 위치, right : 탐색을 종료하는 위치)

1부터 9까지의 숫자가 있다. 이중 3을 탐색한다고 가정해보자.
처음 left는 숫자 후보중 가장 작은 범위인 1이다. right는 역으로 9일 것이다.
이때, 탐색 범위를 반으로 나누는 기준은 (left + right) / 2가 될것이다.

mid = 5가 되며, 내가 탐색하려는 수 "3"이 mid를 기준으로 큰지, 작은지 여부를 판단한다.
이 때, 3은 mid(5)보다 작으니 mid 오른쪽 절반을 범위에서 버린다.
그 후 새로운 탐색 범위를 기존 left ~ mid - 1로 설정한다.

이번엔 mid보다 찾고자 하는"3"이 더 크다.
왼쪽 절반을 탐색 범위에서 제외시키고 기존 left를 mid + 1로 설정한다.
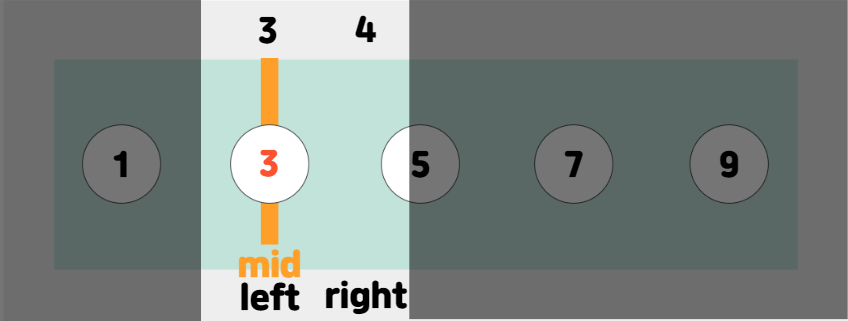
mid가 찾고자 하는 수와 일치한다. 3을 찾았다!
이때, left를 mid+1로 옮기던 right를 mid-1로 옮기던 left < right의 조건을 벗어나기 때문에
반복문(이진탐색)도 종료된다.
풀이 과정
이분 탐색에 대한 정리가 끝났으니, 이제 문제에 대한 로직을 해결해보자.
우리가 찾아야 할 값은 모든 사람이 심사를 받는데 걸리는 시간의 최솟값이다.
그렇다면 시간의 범위는 0 ~ 가장 오래 걸린 심사시간 일 것이다.
left : 0 , right : 모든 사람이 가장 오래걸리는 심사대에서 심사를 받은 시간
1. 먼저 각 심사관 별 심사시간이 담긴 times 배열을 오름차순으로 정렬한다.
2. left = 0, right = times[times.length-1] * n(사람 수)로 설정한다.
3. 이분탐색을 진행한다. 반복문의 제한은 left <= right
3-1. mid 시간을 구한다. (left + right) / 2
3-2. 각 심사대 별로 주어진 시간 mid동안 몇명의 사람을 심사할 수 있는지 합산한다.
(ex. mid = 10, times = {2, 3, 4}인 경우, 10 / 2 + 10 / 3 + 10 / 4로 총 5+3+2=10명 가능
3-3. 심사한 총 사람 수(complete)가 n보다 작을경우,
해당 시간동안 모든 사람을 검사할 수 없다는 뜻이다. left를 mid + 1로 로 이전한다.
3-4. n보다 크거나 같을 경우
answer = mid를 넣어둔다. 다만 해당 경우보다 더 최솟값이 나올 수 있다.
right = mid - 1로 설정하여 범위를 줄여준다.
4. 반복문이 끝나고 answer를 return한다.
왜 complete == n을 따로 빼지 않았을까?
우리가 찾아야 할 값은 "모든 사람을 심사하는 시간의 최솟값"이다. 즉, n과 complete가 딱 맞아떨어지게 같은 경우가 없을 수도 있다. 즉 '여분의 시간'이 남은 채로 모두 심사하는게 최선의 선택일 수도 있다.
따라서 complete >= n일 경우에 answer에 값을 저장해준 후, right의 범위를 줄여보며 더 빠른 시간이 있으면 answer를 바꿔주고, 없다면 반복문을 빠져나와(left > right인 경우) 로직이 끝나게 된다.
풀이 코드
import java.util.Arrays;
class Solution {
public long solution(int n, int[] times) {
long answer = 0;
Arrays.sort(times);
long left = 0;
long right = times[times.length-1] * (long)n; //모든 사람이 가장 느리게 심사받음
while(left <= right) {
long mid = (left + right) / 2;
long complete = 0;
for (int i = 0; i < times.length; i++)
complete += mid / times[i];
if (complete < n) // 해당 시간에는 모든 사람이 검사받을 수 없다.
left = mid + 1;
else {
right = mid - 1;
answer = mid; // 모두 검사받았으나, 더 최솟값이 있을 수 있다.
}
}
return answer;
}
}
이분 탐색을 처음 접하면서 로직이 다소 낯설게 느껴졌다.
연관된 문제를 풀다보니 익숙해지면서 생각보다 쉽게 자리잡았던 것 같다.
이분 탐색을 할 때는
1. 내가 찾아야 할 정답의 범위를 left ~ right로 정한다.
2. 정답을 mid로 간주한 후, 해당 정답이 유효한지 살펴본다.
3. 2번 여부를 따지며 left와 right의 범위를 좁힌다.
4. left > right가 되면 반복을 끝내고 답을 반환한다.
이정도의 로직만 정립하면 어떤 문제가 나와도 비슷할 것 같다!
'알고리즘 > 프로그래머스' 카테고리의 다른 글
| [프로그래머스] 가장 먼 노드-JAVA (0) | 2022.03.19 |
|---|---|
| [프로그래머스] 징검다리-JAVA (1) | 2022.03.19 |
| [프로그래머스] 도둑질-JAVA (0) | 2022.03.10 |
| [프로그래머스] N으로 표현-JAVA (0) | 2022.03.09 |
| [프로그래머스] 여행경로-JAVA (0) | 2022.03.09 |